1. Cel zadania.

2. Model obliczeniowy.

2.1. Analiza modelu obliczeniowego.

               2.1.1 Pierwszym etapem jest analiza rury o średnicy d=800[mm] i grubości ścianki z=10[mm] przy obciążeniu ciśnieniem wewnętrznym P=6.4[MPa]. Przeprowadziłem badanie wpływu zmiany średnicy na naprężenia w zakresie średnic od d=100[mm] do d=1100[mm].

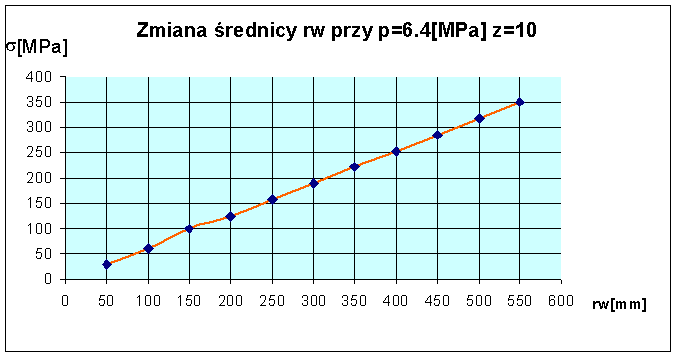
Jak widać z powyższego wykresu naprężenia są wprost proporcjonalne do średnicy rury i mają tendencje rosnącą. Zatem optymalnym i najbardziej korzystnym rozwiązaniem byłoby zastosowanie jak najmniejszej średnicy rury przy zadanych parametrach ( ciśnieniu p=6.4[MPa] i grubości ścianki rury z=10[mm]).

Przykłady obliczeń.

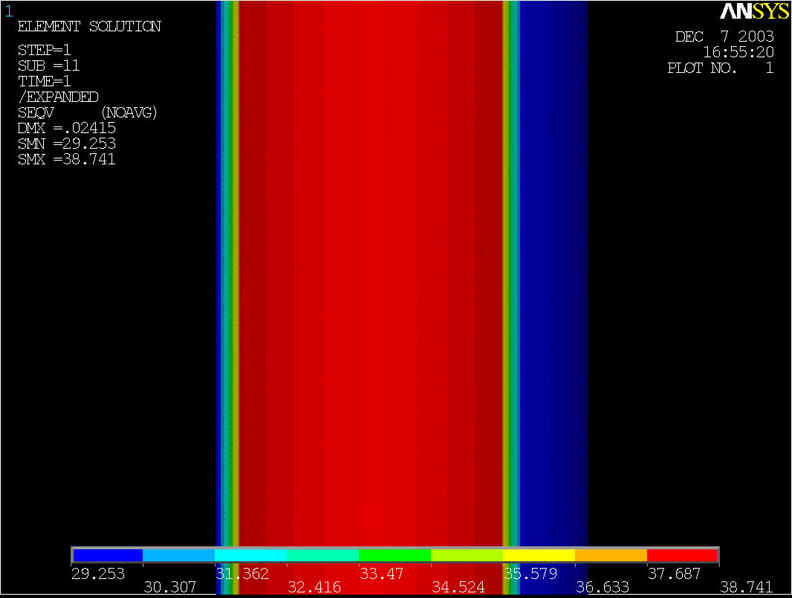
rys.1 Na powyższym rysunku przedstawiony model geometryczny rury, którego średnica  wynosi      d=100[mm] grubość ścianki wynosi z=10[mm] a ciśnienie p=6.4[MPa].

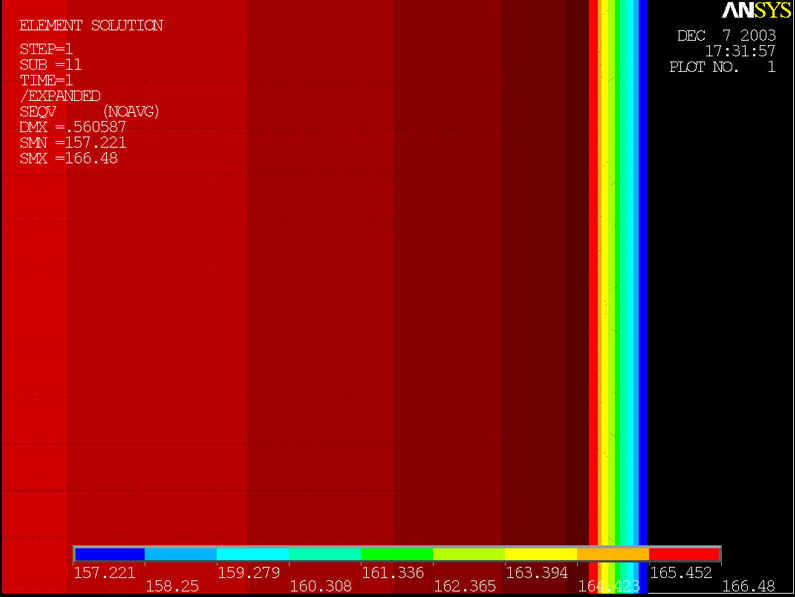
rys.2 Na powyższym rysunku przedstawiony model geometryczny rury, którego średnica  wynosi     d=500[mm] grubość ścianki wynosi z=10[mm] a ciśnienie p=6.4[MPa].

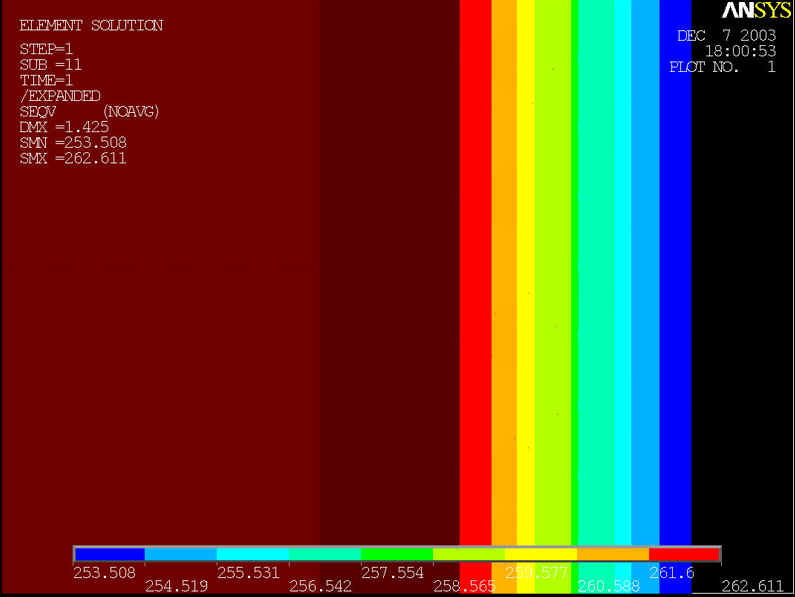
rys.3 Na powyższym rysunku przedstawiony model geometryczny rury, którego średnica  wynosi     d=800[mm] grubość ścianki wynosi z=10[mm] a ciśnienie p=6.4[MPa].

rys.4 Na powyższym rysunku przedstawiony model geometryczny rury, którego średnica  wynosi     d=1100[mm] grubość ścianki wynosi z=10[mm] a ciśnienie p=6.4[MPa].

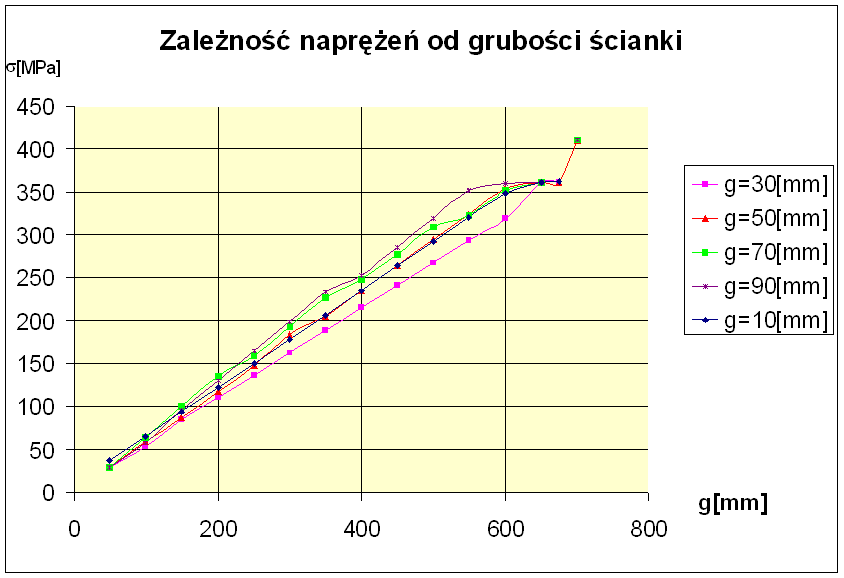
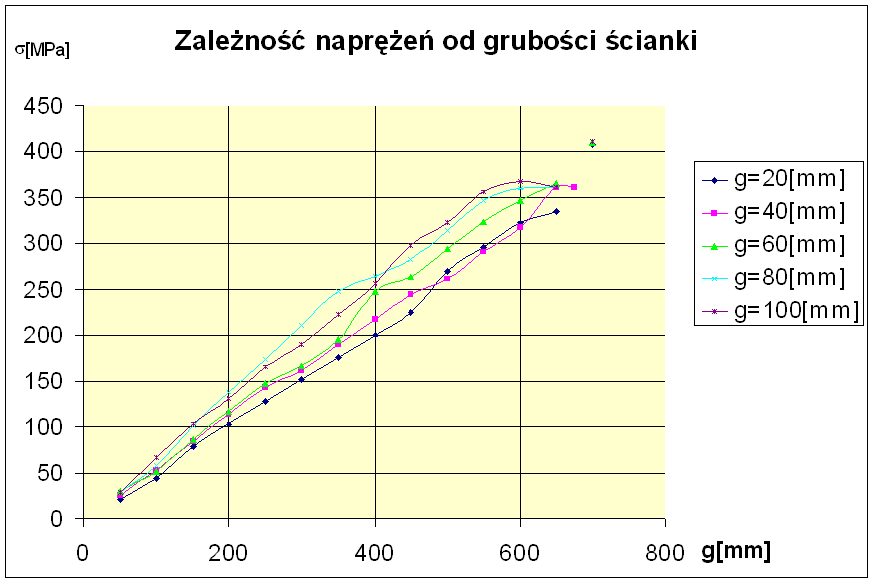
                   2.1.2 Teraz przedstawię wpływ grubości ścianki nakładki rury g na spiętrzenie naprężeń w modelu obliczeniowym przy parametrach optymalnych i zadanych wcześniej gabarytach rury.

Przykłady obliczeń.

W przykładach są tylko zobrazowane tyko te miejsca w których występuje największe spiętrzenie naprężeń czyli w miejscu powstania karbu na skutek nałożenia nakładki na rurę.

rys.5 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi d=100[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=100[mm] przy ciśnieniu p=6.4[MPa].

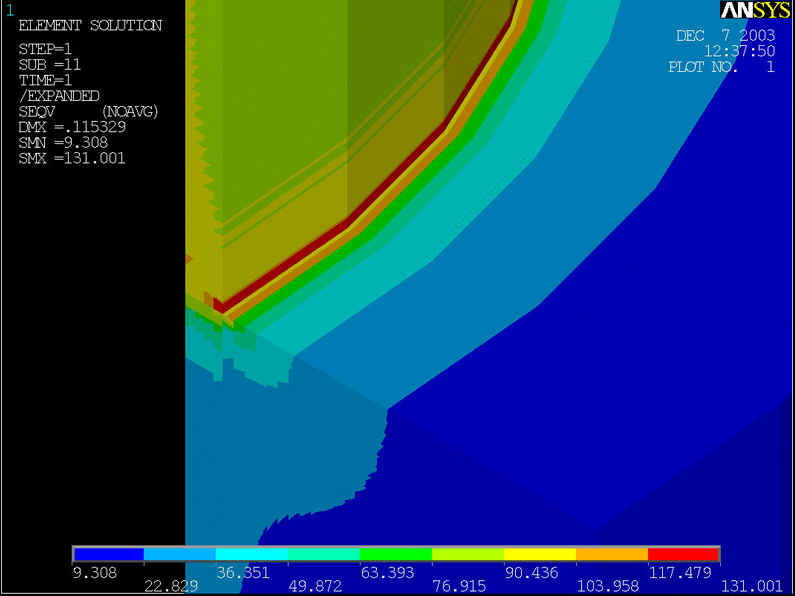
rys.6 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi             d=400[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=100[mm] przy ciśnieniu p=6.4[MPa].

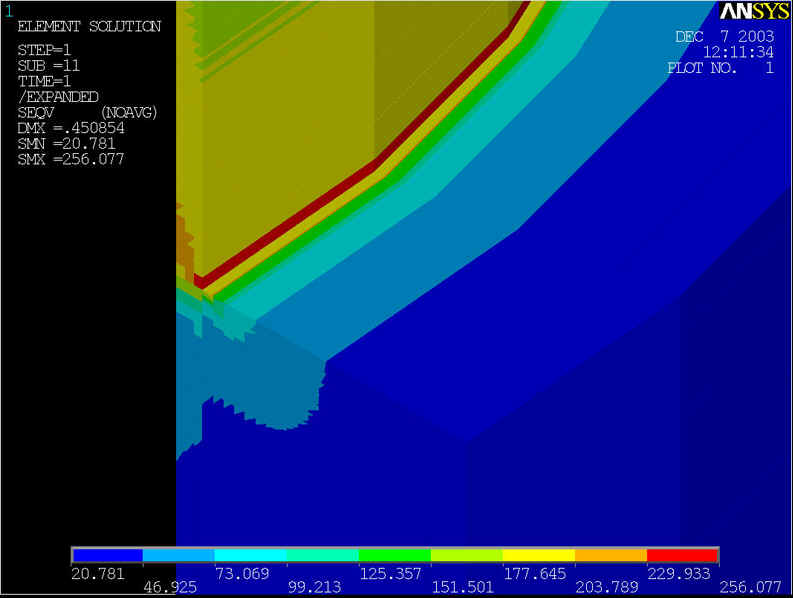
rys.7 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi             d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=100[mm] przy ciśnieniu p=6.4[MPa].

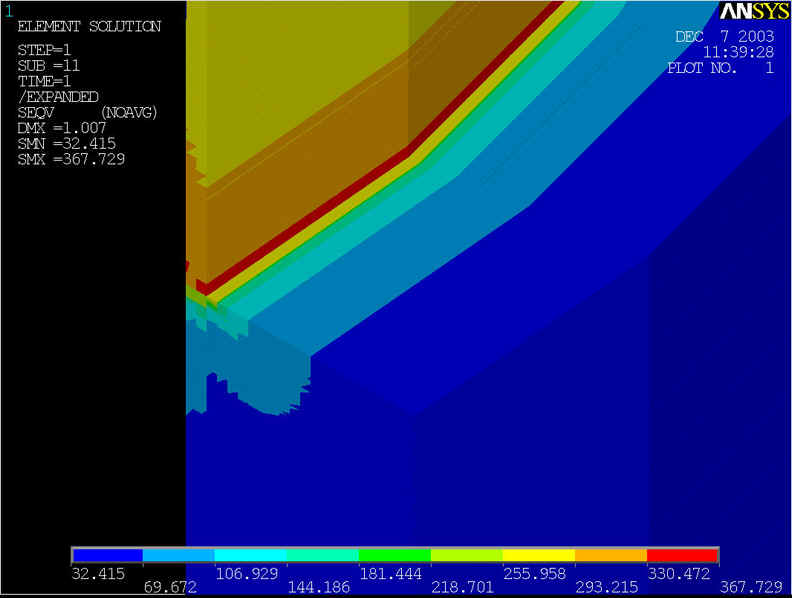
rys.8 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                 d=1200[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=100[mm] przy ciśnieniu p=6.4[MPa].

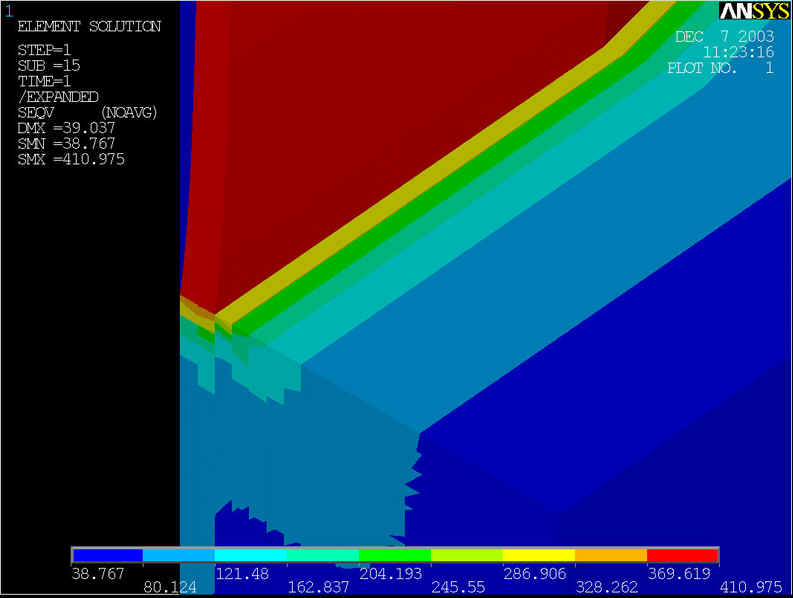
rys.9 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                 d=1400[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=100[mm] przy ciśnieniu p=6.4[MPa].

2.1.3 Teraz przedstawię wpływ zmiany ciśnienia na spiętrzenie naprężeń w modelu obliczeniowym przy parametrach optymalnych i zadanych wcześniej gabarytach rury.

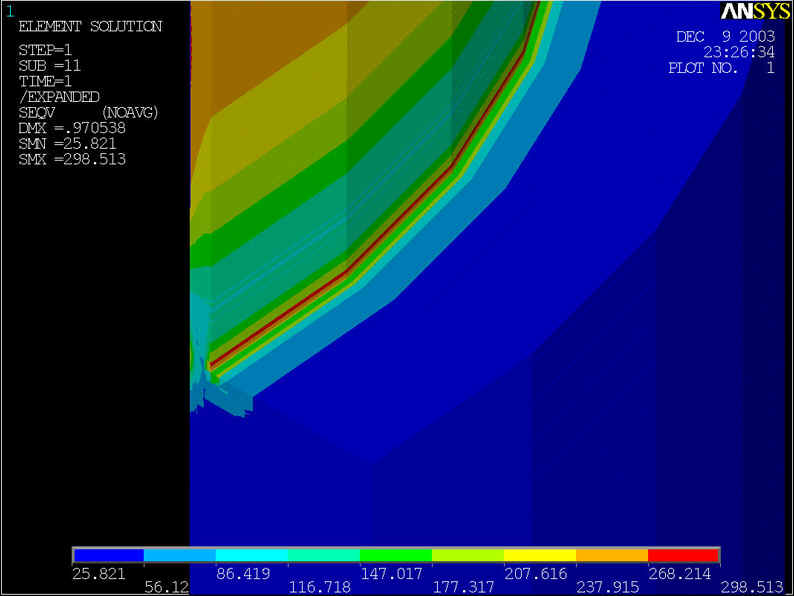
rys.10 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=75[mm] przy ciśnieniu p=6.4[MPa].

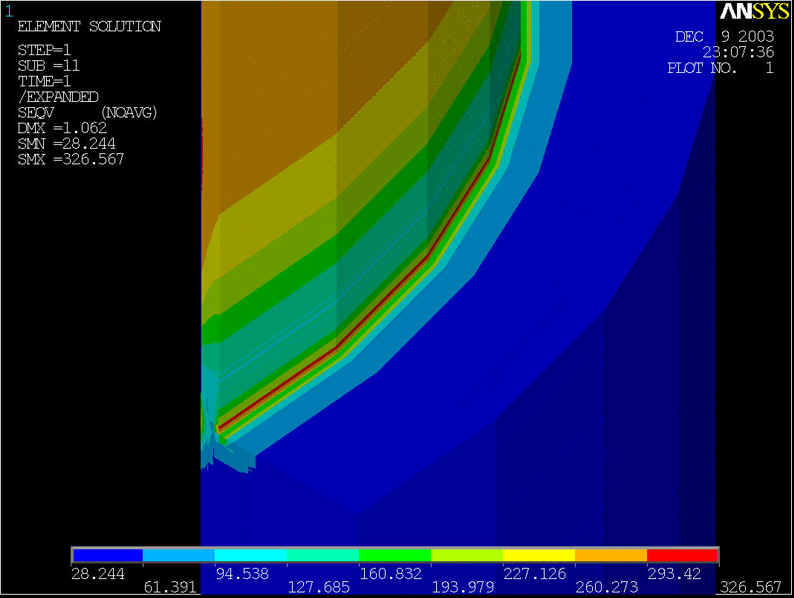
rys.11 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=75[mm] przy ciśnieniu p=7.0[MPa].

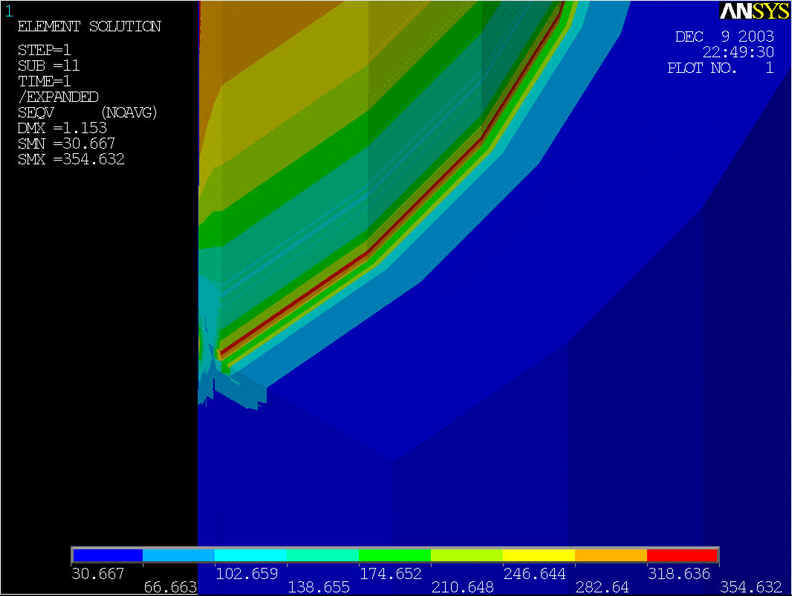
rys.12 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=75[mm] przy ciśnieniu p=7.6[MPa].

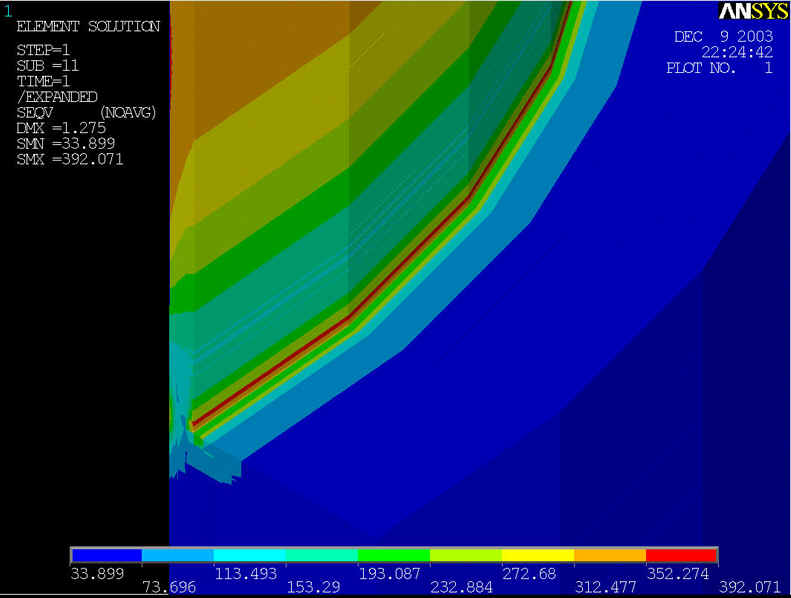
rys.13 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=75[mm] przy ciśnieniu p=8.4[MPa].

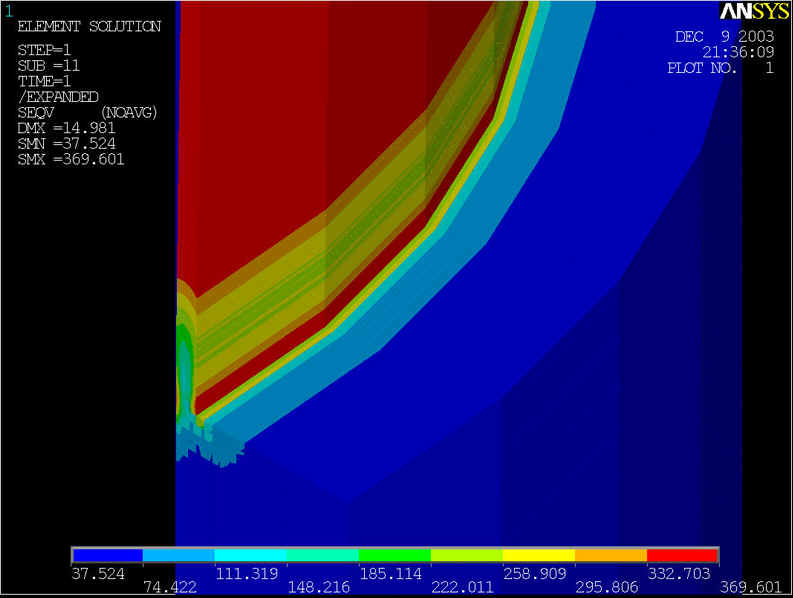
rys.14 Na powyższym rysunku przedstawiony model geometryczny, którego średnica rury wynosi                d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=75[mm] przy ciśnieniu p=9.2[MPa].

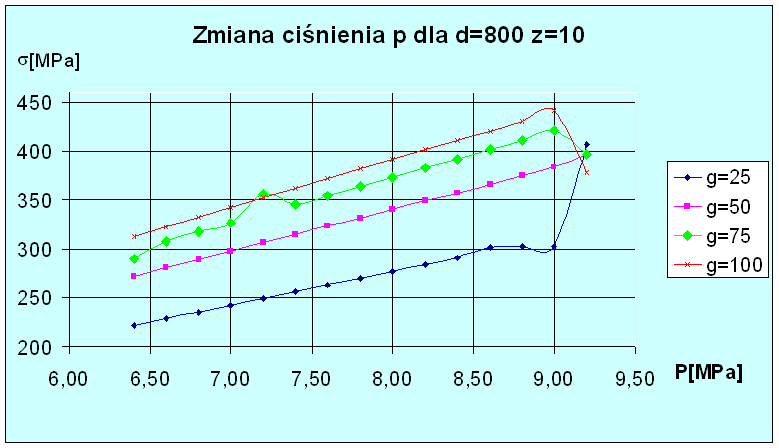
           Na powyższym wykresie przedstawione są zależności dla modelu nie zmodyfikowanego przy następujących parametrach: średnica rury d=800[mm], grubość ścianki rury z=10[mm] dla grubości nakładki rury g=25[mm], g=50[mm], g=75[mm], g=100[mm], przy zmieniającym się ciśnieniu w zakresie od p=6.4[MPa] do p=9.2[MPa], które zmienia się co 0,2[MPa]. Analizując powyższy wykres można wybrać najbardziej optymalne rozwiązanie dla naszego przypadku. Kryterium wyboru jest stosunkowo najniższe naprężenie albowiem ono zapewnia poprawną pracę konstrukcji bez obawy jej zniszczenia. Zatem najbardziej korzystnym przypadkiem jest ten dla którego g=25[mm]. Nie mniej jednak naprężenia najmniejsze dla tego przypadku wynoszą w granicach 220[MPa] co przekracza dopuszczalną wartość 135[MPa] dla spoiny dlatego model należy poddać modyfikacji.

2.2. Modyfikacja modelu obliczeniowego.

Modyfikacja modelu obliczeniowego polegała na wykonaniu faz po obu stronach nakładki rury, co spowodowało większą podatność i elastyczność nakładki rurociągu prowadzącego do wyeliminowania naprężeń w strefie spoiny. Poniżej przedstawiony został zarys optymalnego modelu.

2.2.1 Analiza modelu obliczeniowego zoptymalizowanego.

              Analiza badanego modelu polegała na zmianie ciśnienia p w zakresie od p=6.4[MPa] do p=9.4[MPa] zmieniającego się co 0.2[MPa], średnicy rury d=800[mm], grubości ścianki rury z=10[mm], wysokości końca fazy nakładki s=5[mm] dla następujących grubości nakładki: g=25[mm], g=50[mm], g=75[mm] i g=100[mm]. 

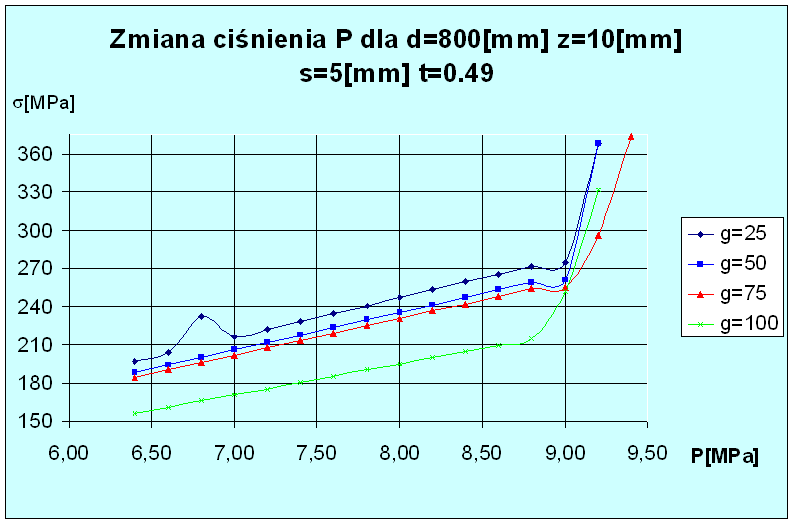
Na podstawie powyższego wykresu można stwierdzić, że najbardziej korzystne warunki pracy rurociągu można uzyskać dla grubości nakładki rury g=100[mm]. 

Przykłady obliczeń.

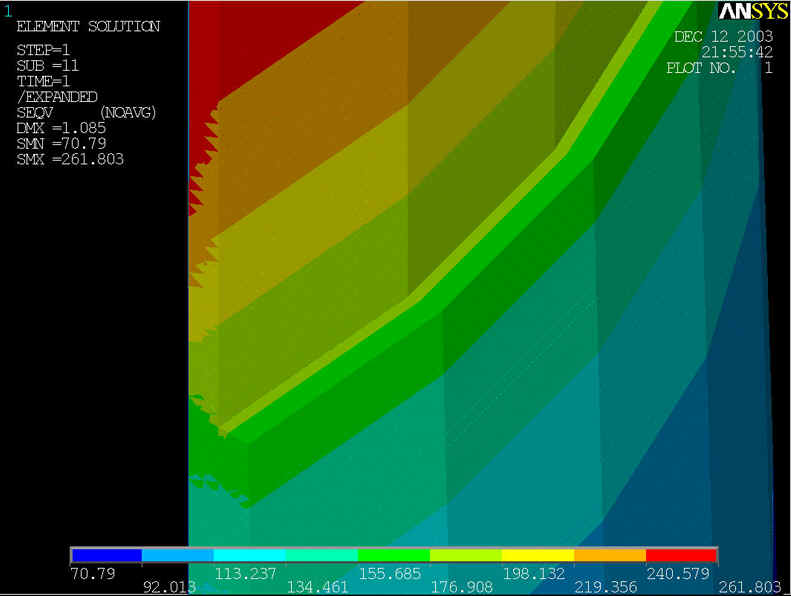
rys.15 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=25[mm] przy ciśnieniu p=6.4[MPa] i s=5[mm]

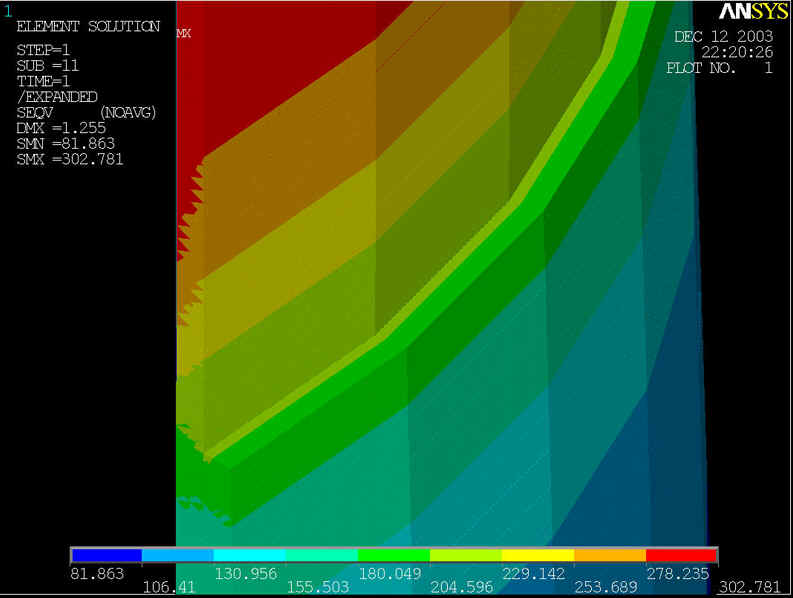
rys.16 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=25[mm] przy ciśnieniu p=7.4[MPa] i s=5[mm].

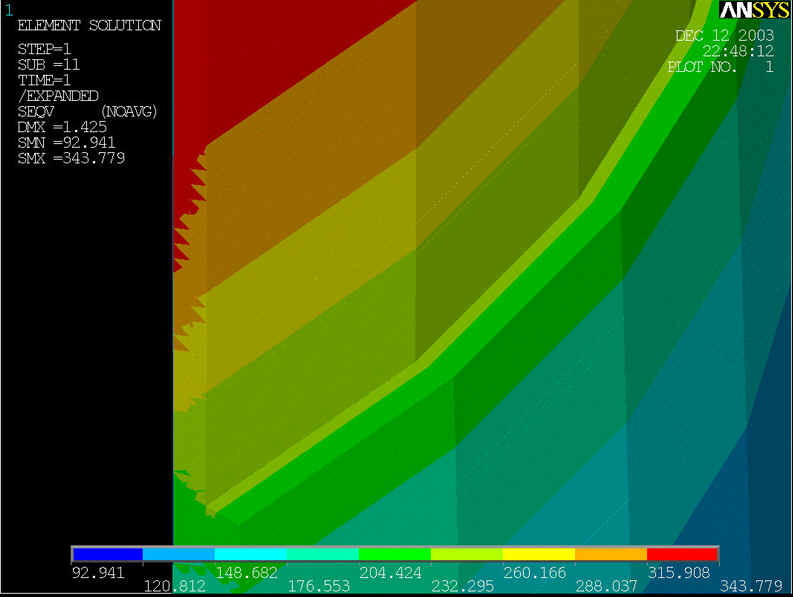
rys.17 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=25[mm] przy ciśnieniu p=8.4[MPa] i s=5[mm].

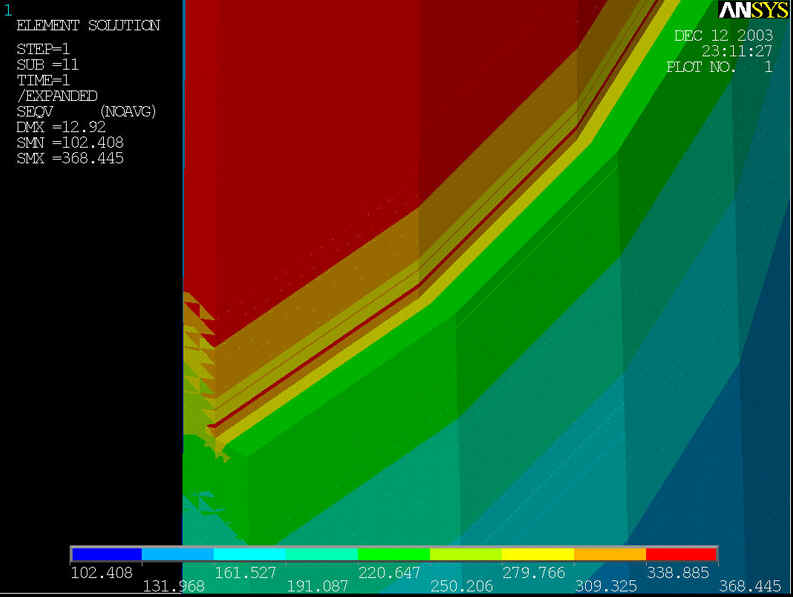
rys.18 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=25[mm] przy ciśnieniu p=9.2[MPa] i s=5[mm].

W celu dobrania bardziej korzystnego modelu obliczeniowego wykonałem badanie dla modelu obliczeniowego zmodyfikowanego zmieniając parametr wysokości końca fazy s (dla s=10[mm]) przy pozostałych parametrach bez zmian ( z=10[mm], d=800[mm] i ciśnieniu p zmieniającym się w zakresie od p=6.4[MPa] do p=9.2[MPa] ulegającego zmianie co 0.2[MPa]). Poniżej zostały przedstawione wyniki badań.

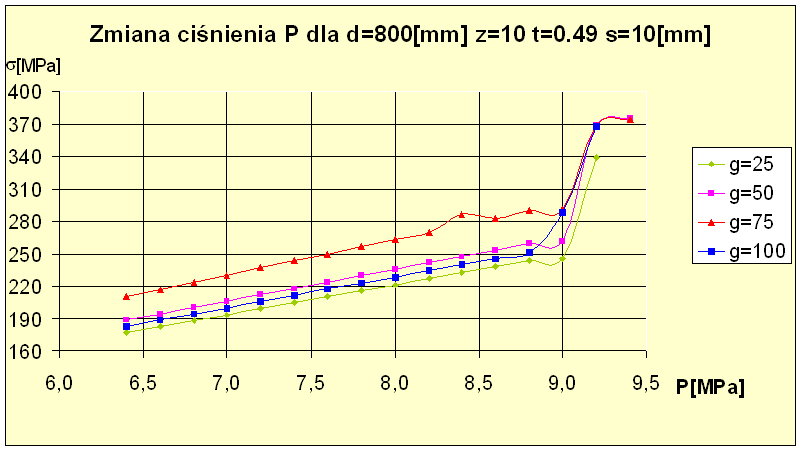
Przeprowadziłem bardziej dogłębna analizę i porównałem wyniki obliczeń dla modelu obliczeniowego zoptymalizowanego i nie zoptymalizowanego oto one:

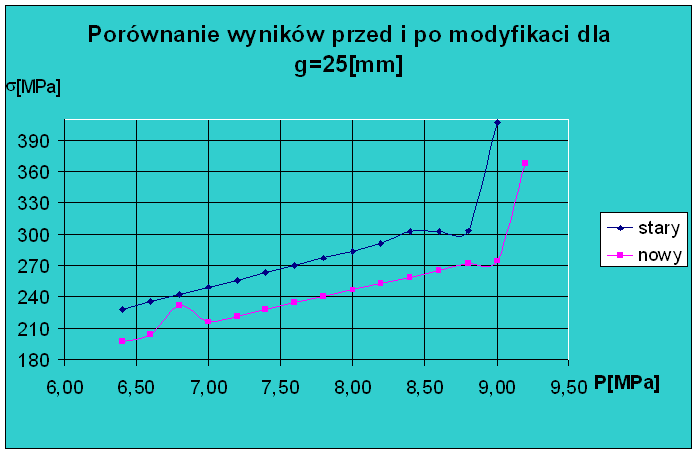
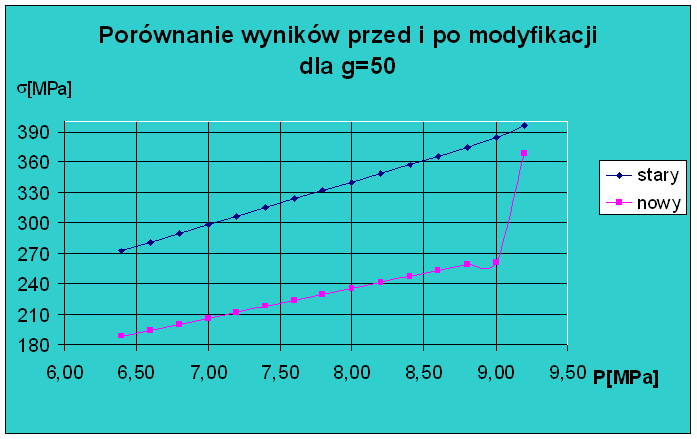
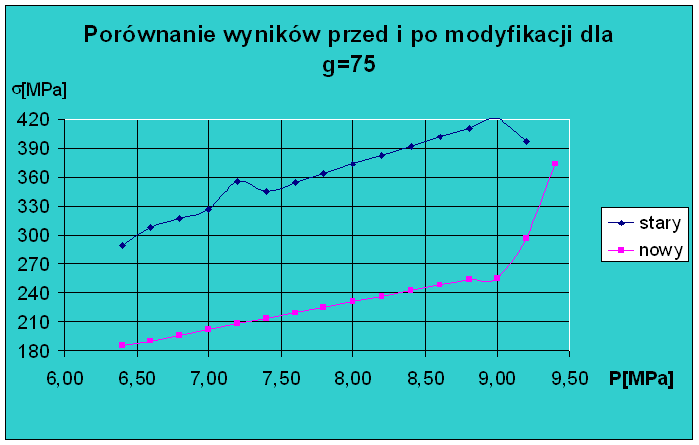
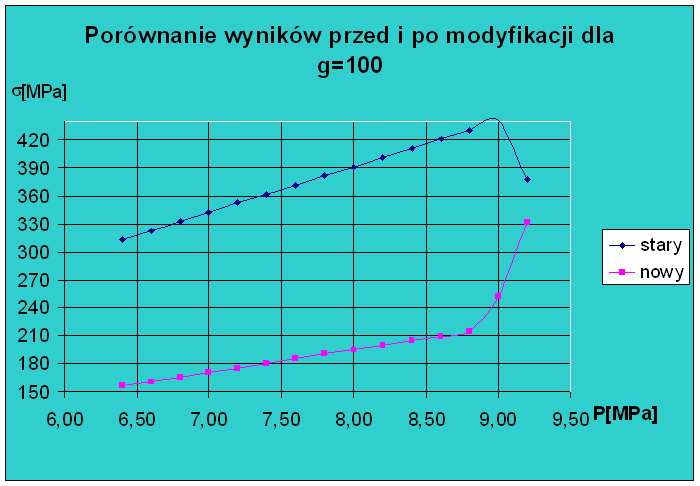
Analizując powyższe wykresy jednoznacznie można powiedzieć, ze model zmodyfikowany daje lepszy wynik aniżeli model przed modyfikacją w całym zakresie. Różnice pomiędzy nimi wynoszą od 20[MPa] dla g=25[mm] do180[MPa] dla g=100[mm].

Dokonałem również porównania modelu zmodyfikowanego dla s=5[mm] i s=10[mm] przy pozostałych parametrach niezmienionych (standardowych). Oto wyniki z analizy.

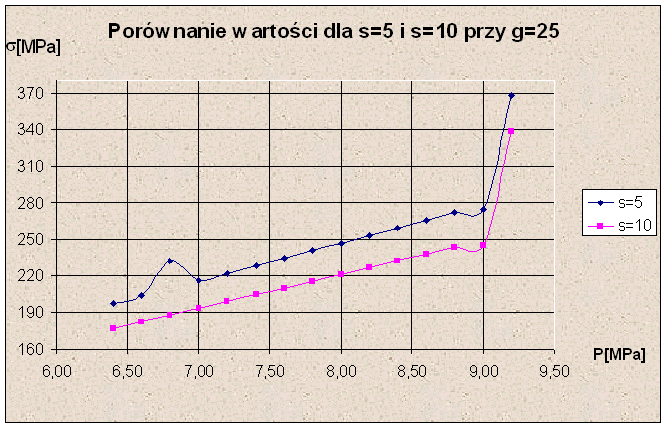
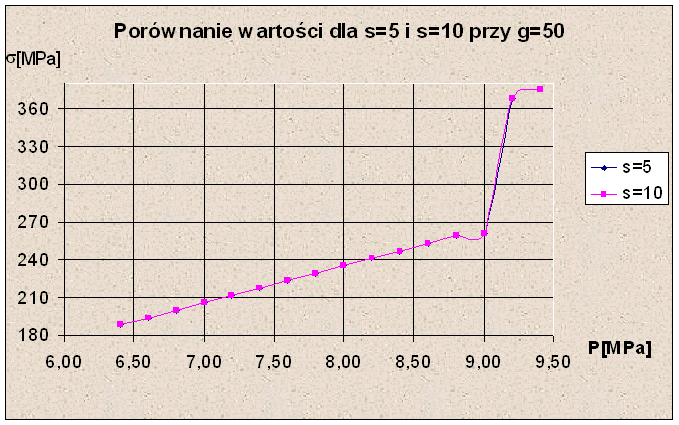
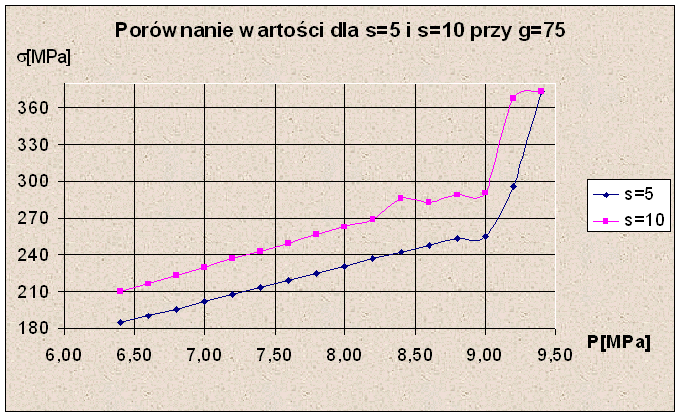
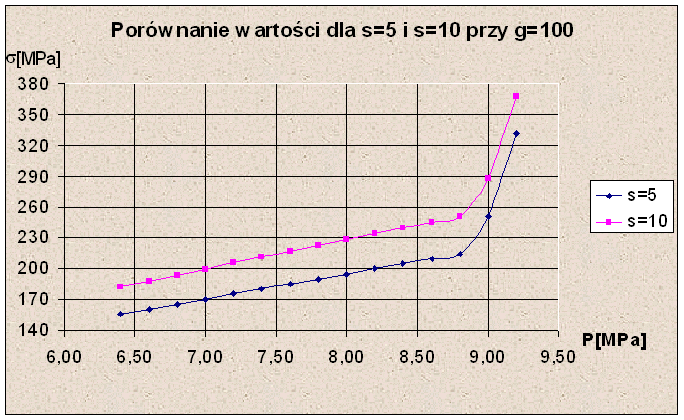
Analizując powyższe wykresy można stwierdzić, że lepsze wyniki dla s=10[mm] uzyskamy dla g=25[mm]. Natomiast dla g=50[mm] wyniki się pokrywają. Dla wartości g=75[mm] i g=100[mm] uzyskamy lepsze rezultaty dla s=5[mm]. Zatem wybór należy dokonać w taki sposób aby wyniki były najkorzystniejsze dla panujących warunków.

              Kolejnym etapem analizy jest badanie zachowania się modelu dla zmiennej długości fazy t. Parametr t określa procentową wartość długości nakładki na rurę. Poniżej zostały przedstawione wyniki z przeprowadzonych badań. Model ten uwzględnia również spoinę. Badanie zostało przeprowadzone dla parametrów standardowych dla grubości nakładki rury g=50[mm] i g=100[mm].

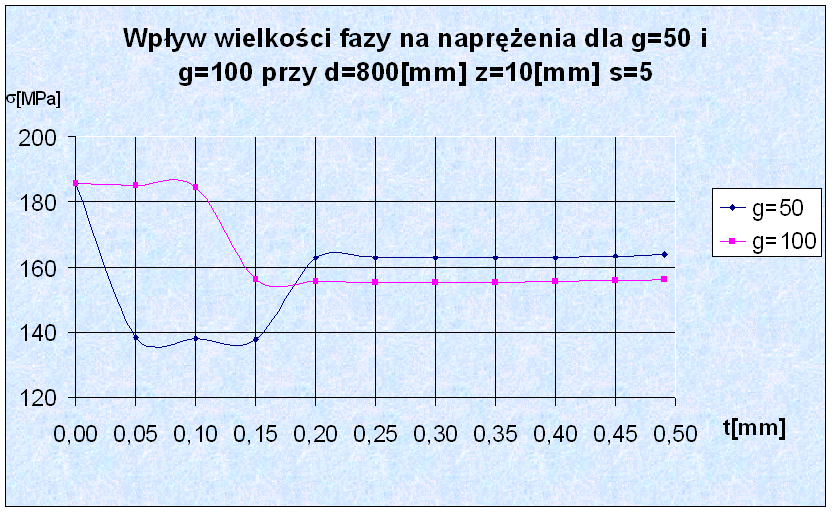
Przykłady obliczeń.

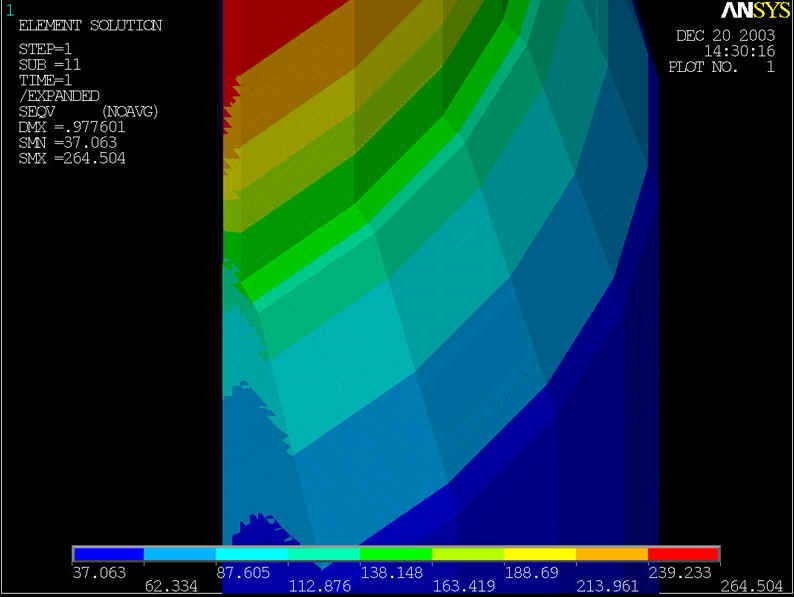
rys.19 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=50[mm] przy ciśnieniu p=6.4[MPa] i s=5[mm] i t=0.1 długości nakładki.

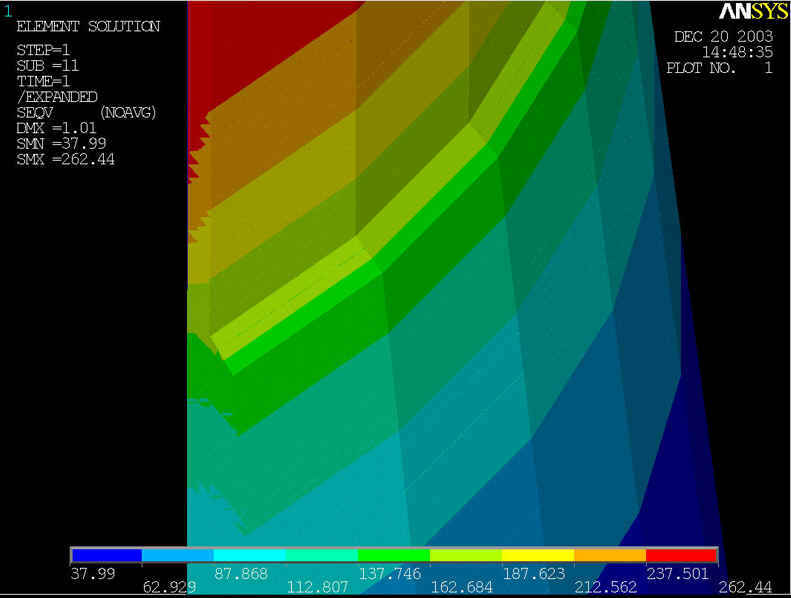
rys.20 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=50[mm] przy ciśnieniu p=6.4[MPa] i s=5[mm] i t=0.3 długości nakładki.

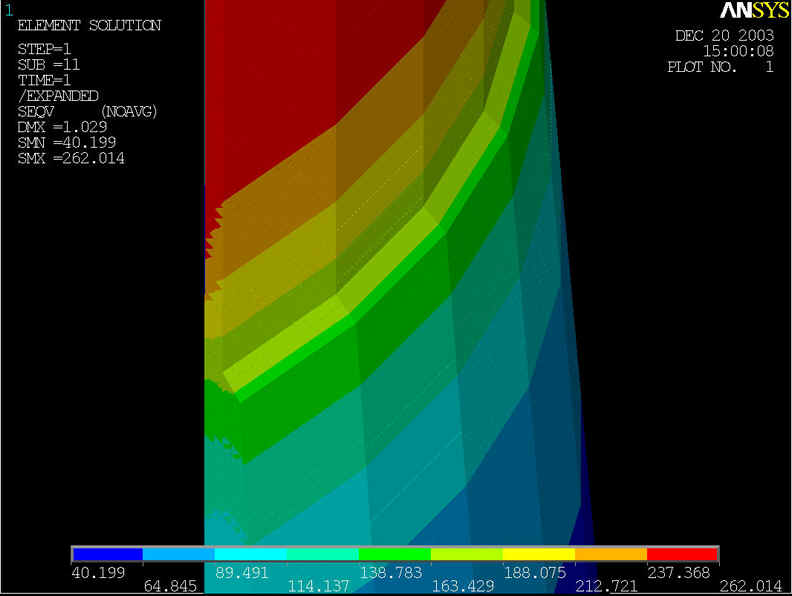
rys.21 Na powyższym rysunku przedstawiony model geometryczny zmodyfikowany, którego średnica rury wynosi d=800[mm] grubość ścianki wynosi z=10[mm], grubość nakładki g=50[mm] przy ciśnieniu p=6.4[MPa] i s=5[mm] i t=0.45 długości nakładki.

2.2. Wnioski.

           Podsumowując  powyższe informacje można dojść do wniosku, że cel zadania został spełniony gdyż uzyskaliśmy optymalne  naprężenia w miejscu najbardziej narażonym. Należy jednak pamiętać aby odpowiednio dobrać parametry i gabaryty konstrukcji co wiąże się z pewnymi odstępstwami od zalecanych rozwiązań. Nie mniej jednak można uzyskać żądany cel stosując zaawansowane programy obliczeniowe do których można zaliczyć ANSYSA. Umożliwia on w miarę dokładnie i szybko, w porównaniu z metodami klasycznymi dokonać obliczeń inżynierskich, postawić diagnozę i dokonać ewentualnych modyfikacji. Wymaga on jednak zawansowanej obsługi i jest czasochłonny a i tak jest stosowany ze względu na swoje zalety.