zadanie 1

Modelowanie powłokowe (z uwzględnieniem dużych przemieszczeń)

Zadanie studialne: kątownik podparty wspornikowo (zamocowany w ścianie), obciążony jedynie swoim ciężarem.

model bryłowy

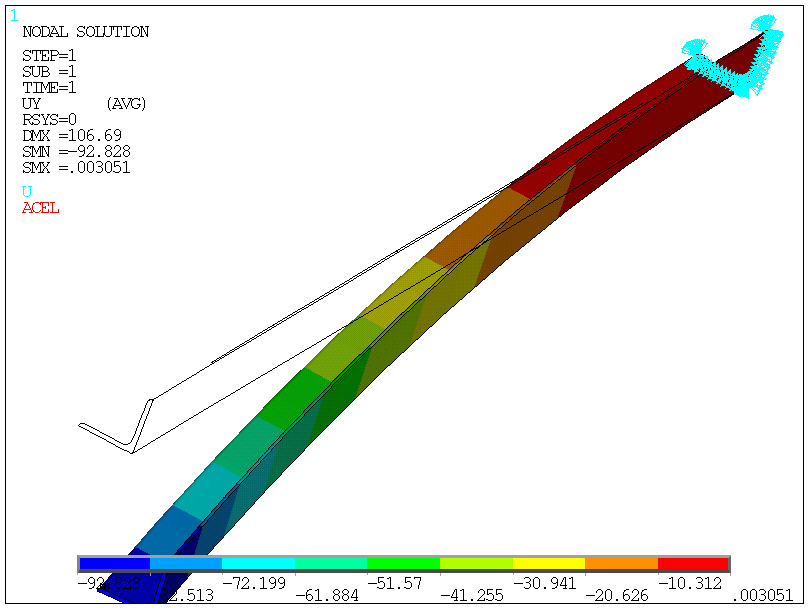
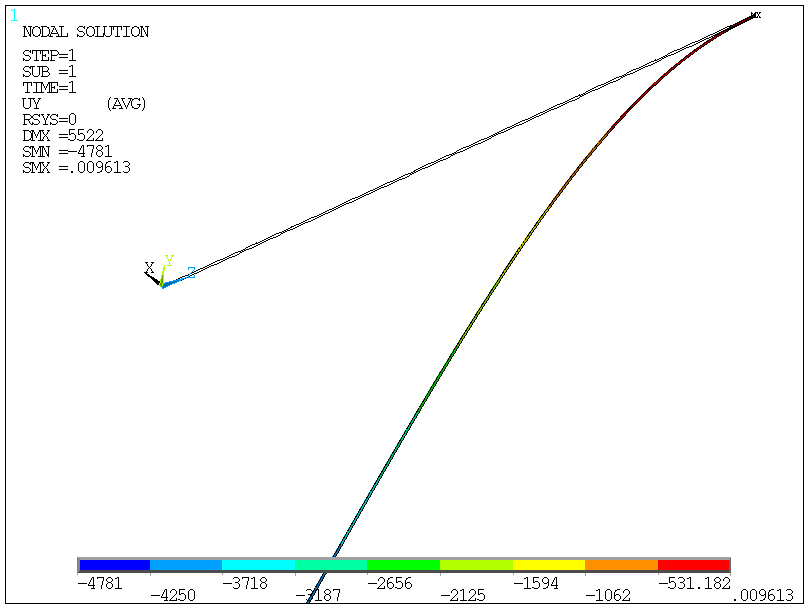
ugięcie metrowego fragmentu (z podparciem)

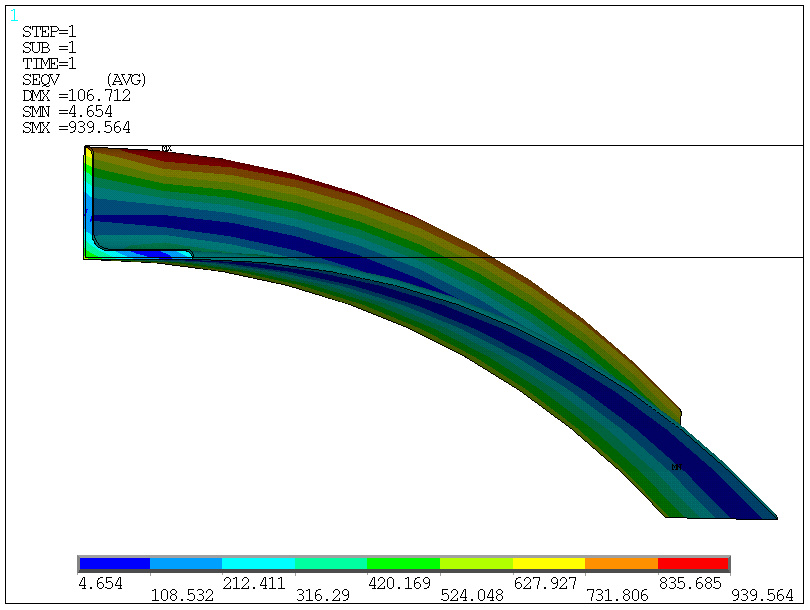
metrowy fragment: naprężenia (obrót przekroju)

model bryłowy (92 tys. węzłów po 3 stopnie swobody) - czas obliczeń: 104 sekundy

model powłokowy

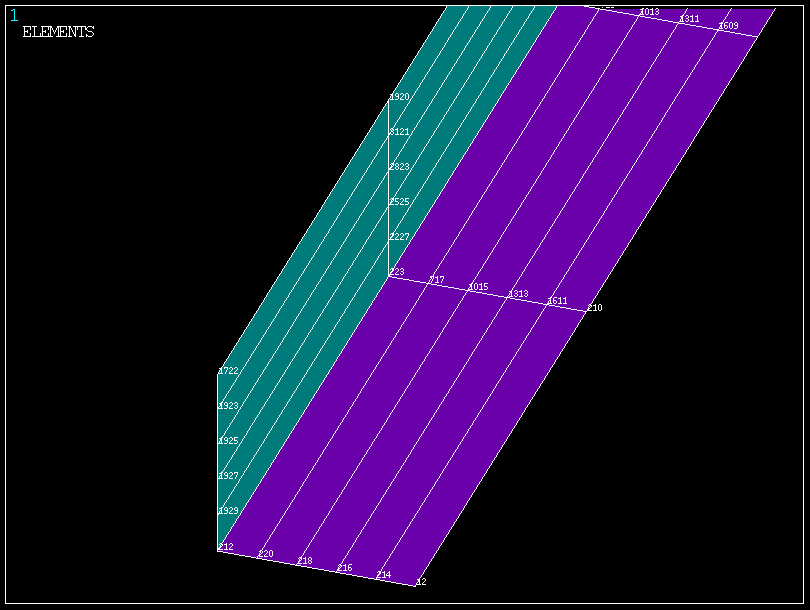
model geometryczny

podział na elementy skończone

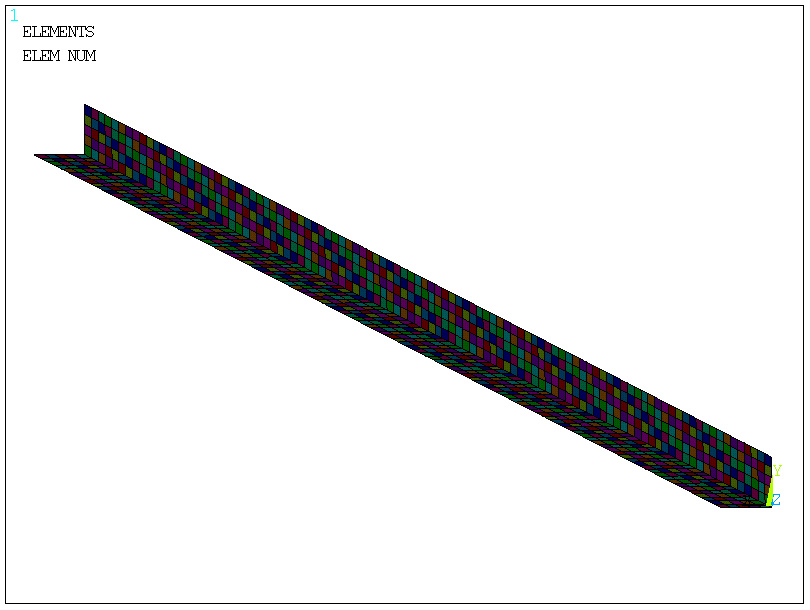
brak grubości elementu jako wymiaru!

można wykorzystać parametr do obrazu graficznego: /ESHAPE,1.0

podparcie

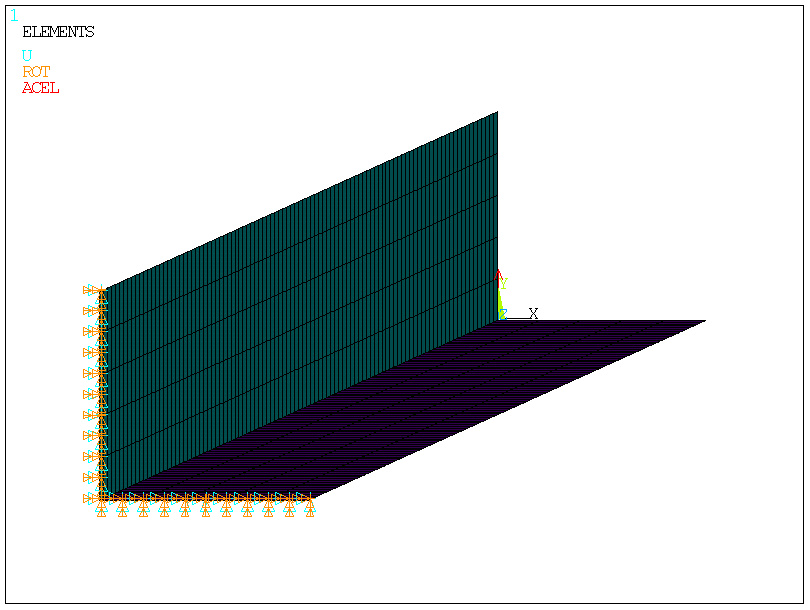
po obciążeniu grawitacją: ACEL,0,9.81,0
(dodatkowo należy zdefiniować gęstość: MP,DENS,1,7.81E-6)

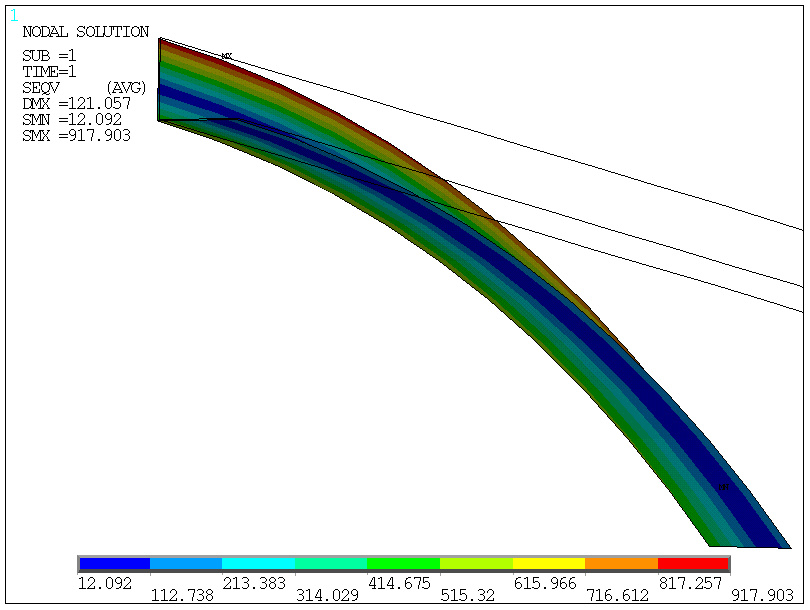
zgodność wyników z modelem bryłowym
naprężenia zredukowane wg Hubera (największe)

model powłokowy: 918 MPa
model bryłowy: 940 MPa

(2.3% różnicy) model powłokowy nie uwzględnia karbów związanych ze zmianą grubości blachy!

dużo mniejsze nakłady obliczeniowe

model powłokowy: 3.2 tys. węzłów po 6 stopnie swobody=19 tys. równań; czas obliczeń: 4 sekundy
model bryłowy: 92 tys. węzłów po 3 stopnie swobody=276 tys. równań; czas obliczeń: 104 sekundy

lekki obrót końcowego przekroju
(obserwowane jako nierównomierne przemieszczenie w kieunku X)

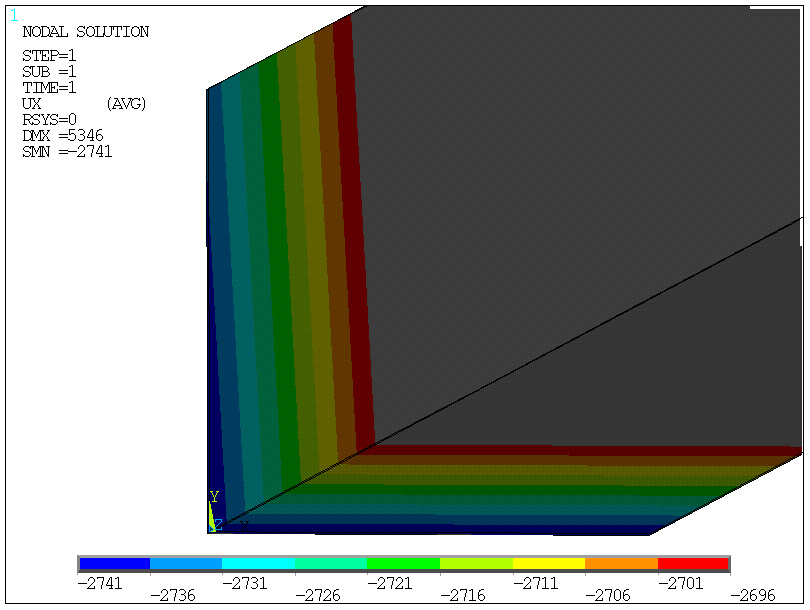
(obserwowane jako nierównomierne przemieszczenie w kieunku X)

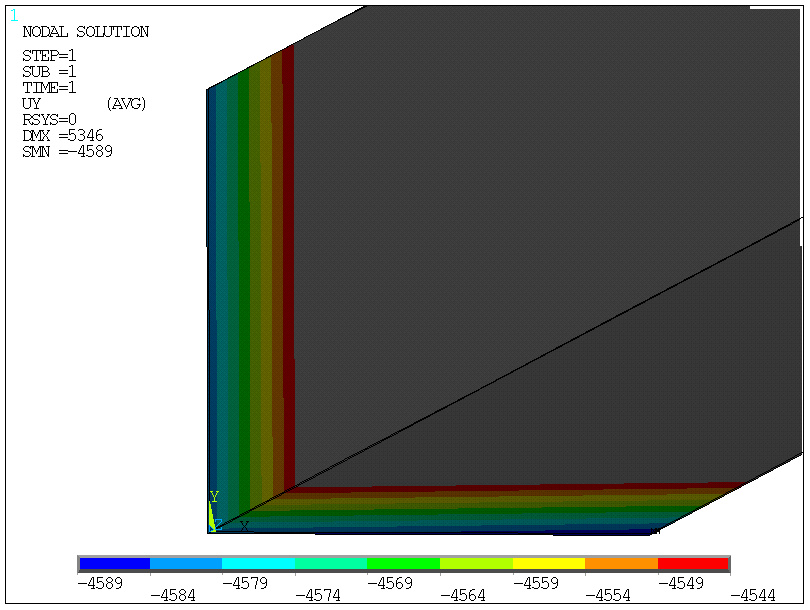
Zróżnicowanie przemieszczenia Y końcowego przekroju świadczy także o niewielkim "rozgięciu" kątownika (spada moment bezwładności przekroju!)

Badanie stateczności teownika

obliczenia w 400 podkrokach, w każdym podkroku:

sumowanie przemieszczeń węzłów, wyliczonych w poprzednim podkroku - z ich położeniem,
niewielkie powiększanie obciążenia

plik duze2.mac:

/SOLU
ANTYPE,0 ! analiza statyczna
NLGEOM,ON !włączenie obliczeń we wspomnianych podkrokach, z kumulowaniem przemieszczeń węzłów
NSUBST,400,400,400 ! podział obliczeń na jednakowe podkroki obliczeniowe
OUTRES,ALL,ALL
FINISH

-pierwszy podkrok, 1/400=0.0025 obciążenia (0.25%)

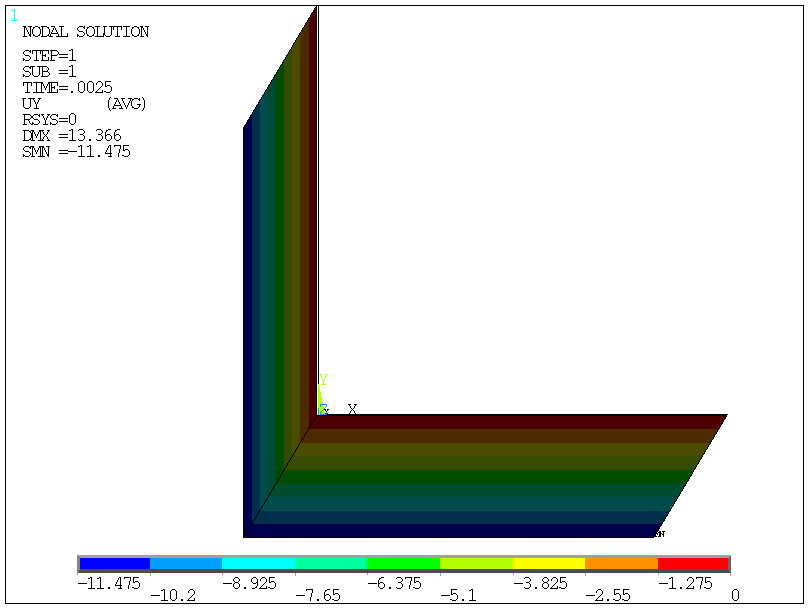
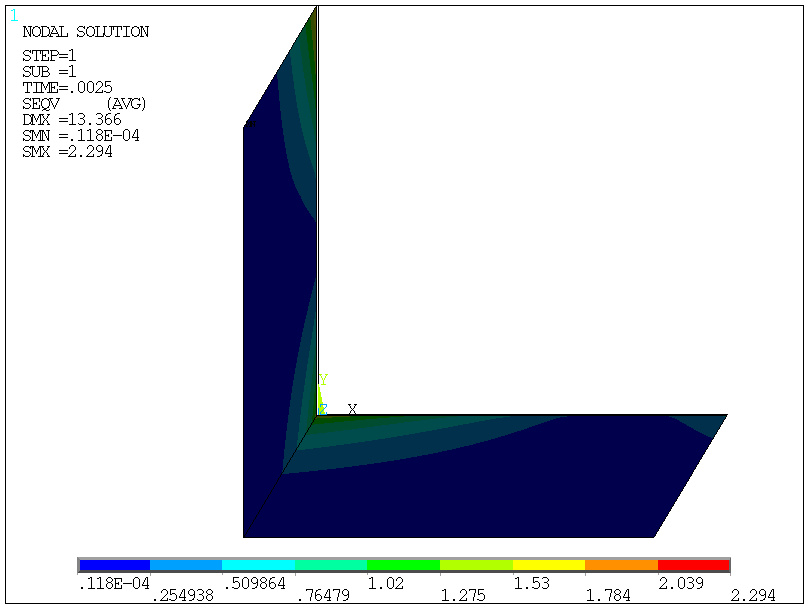
-drugi podkrok, 2/400=0.0050 obciążenia (0.5%)

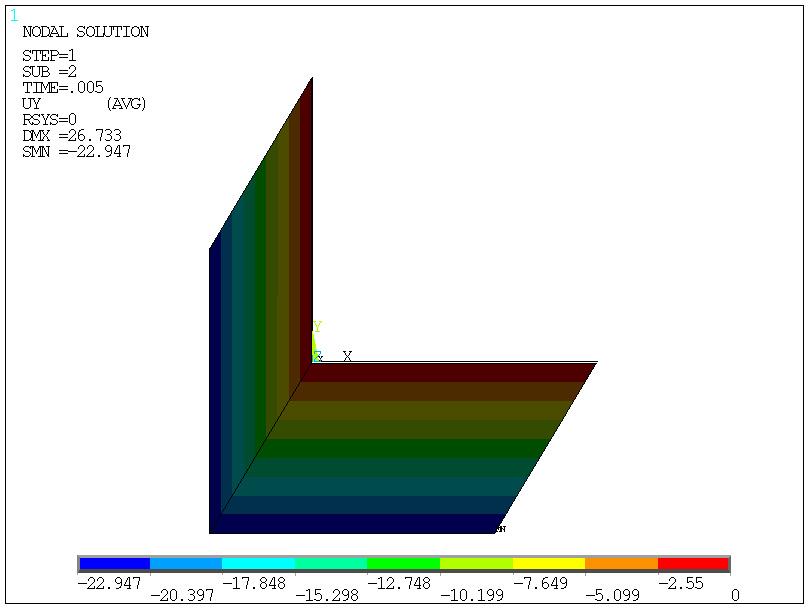
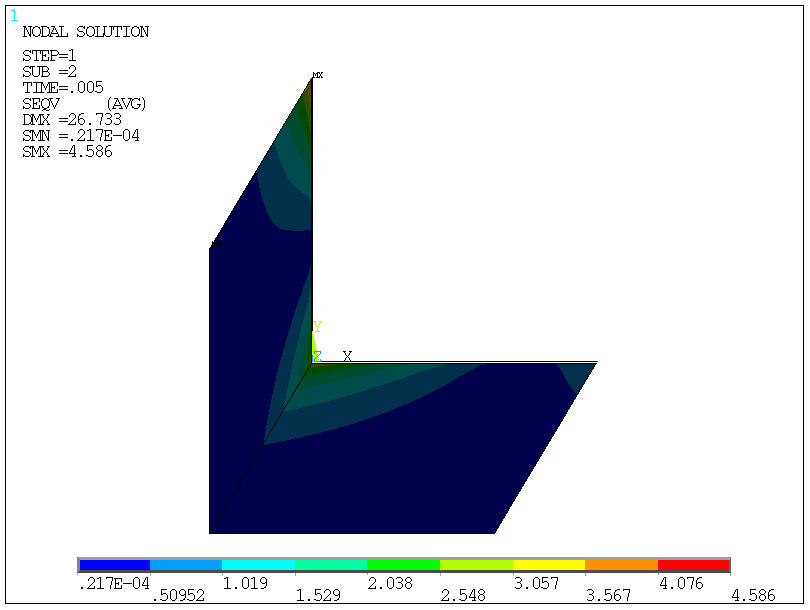
... i tak dalej, np. połowa obciążenia, 200/400=0.50 obciążenia (50%)

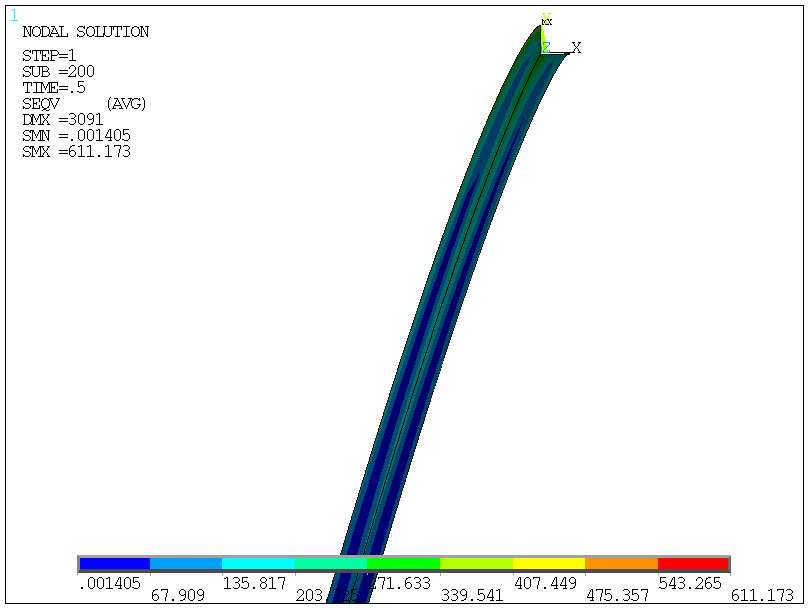
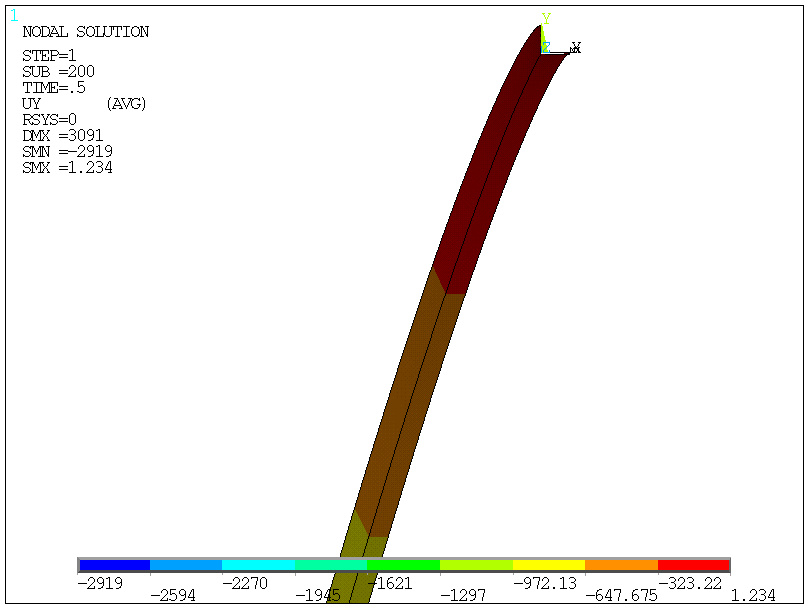
... i w końcupełne obciążenie 400/400=1.0 obciążenia (100%)

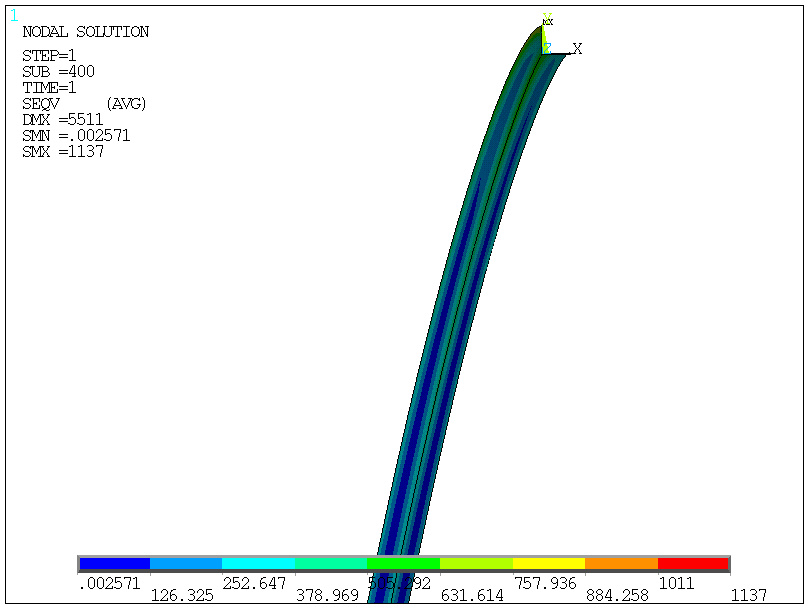
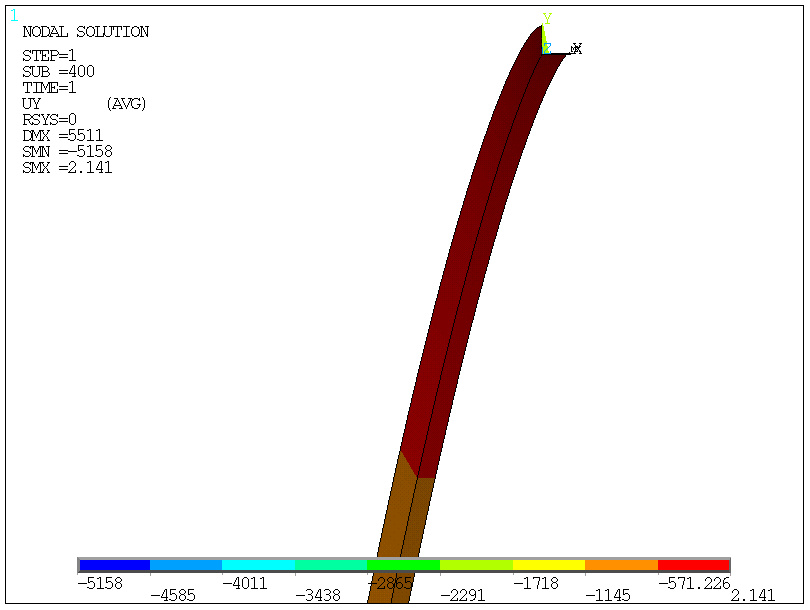
zwykłe obliczenia statyczne (NLGEOM,OFF) wykazały jedynie ugięcie UY=-4589 i naprężenia zredukowane szr=917 MPa

Badanie wpływu obciążenia na zachowanie się konstrukcji

ustalenie numeru węzła w interesującym miejscu konstrukcji

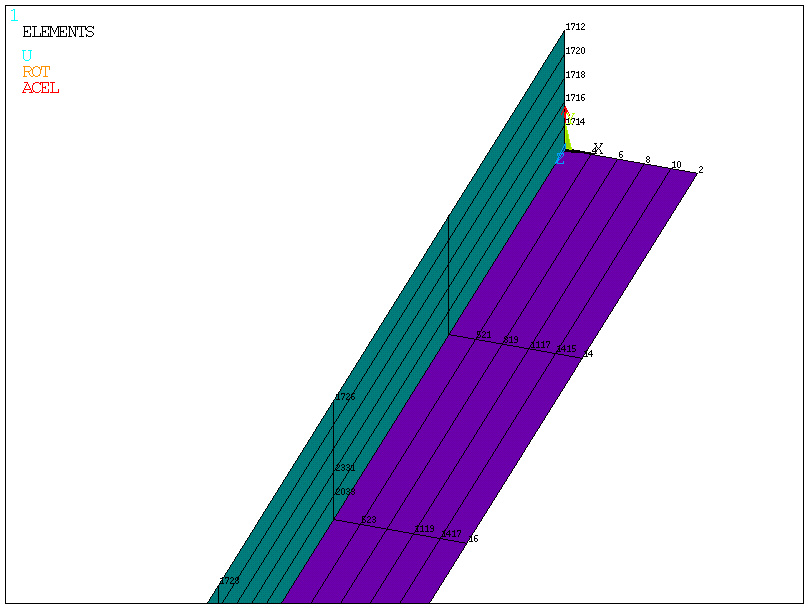
zależność odkształcenia od przemieszczenia

/POST26
NSOL,2,2,U,Y,UY_wez._2
NSOL,3,2,U,X,UX_wez._2
PLVAR,2,3
FINISH

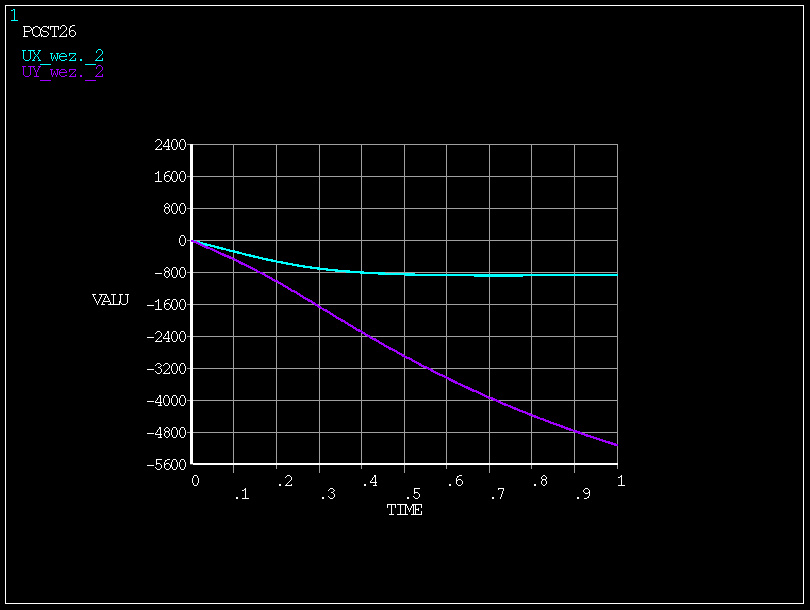
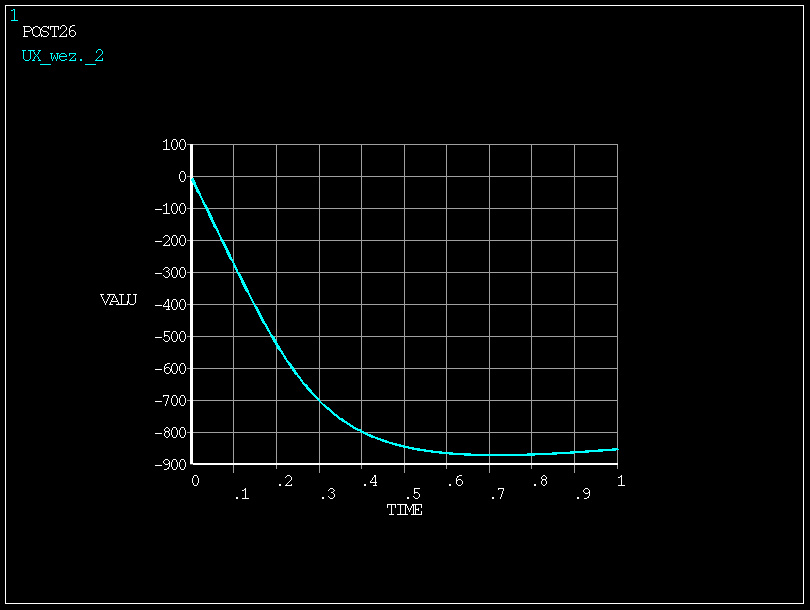
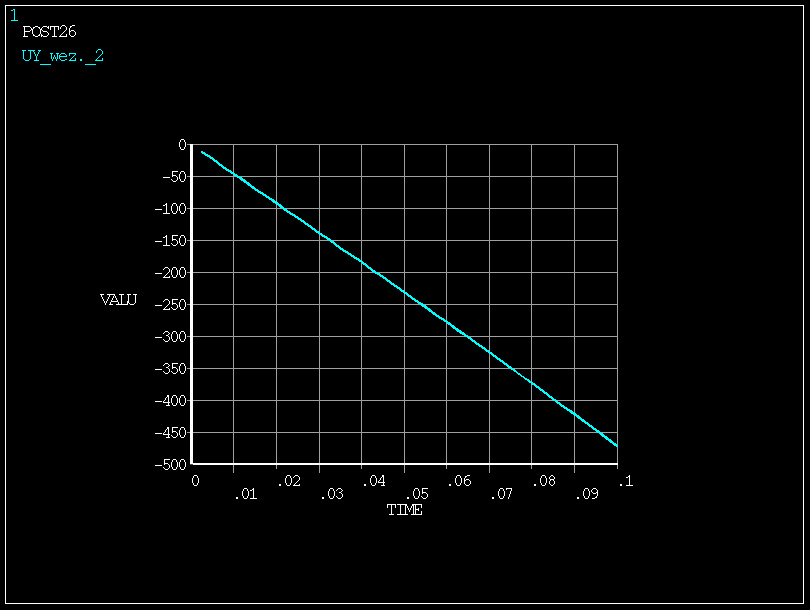
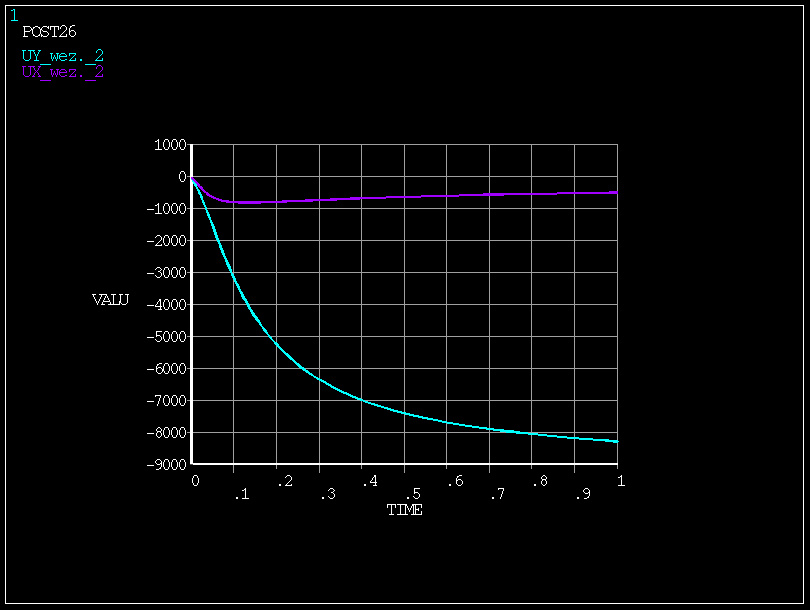
w zakresie obciążenia 0÷0.1 (zmiana obciążenia o 10%) - zmiana odkształcenia UY o 470 mm

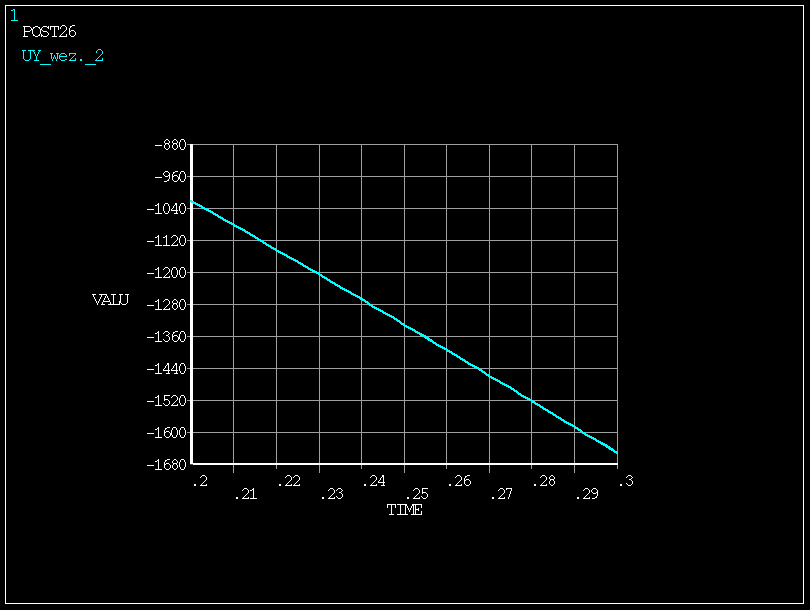
w zakresie obciążenia 0.2÷0.3 (zmiana obciążenia także o 10%) - zmiana odkształcenia UY o 640 mm

zmiana sztywności w wyniku obciążenia o 36% - konstrukcja zachowuje się nieliniowo!

Wpływ obciążenia na wytężenie materiału

ustalenie numeru węzła w miejscu najbardziej obciążonym

/POST26
NSOL,4,1722,S,EQV,S_EQV_w.1722
PLVAR,4
FINISH

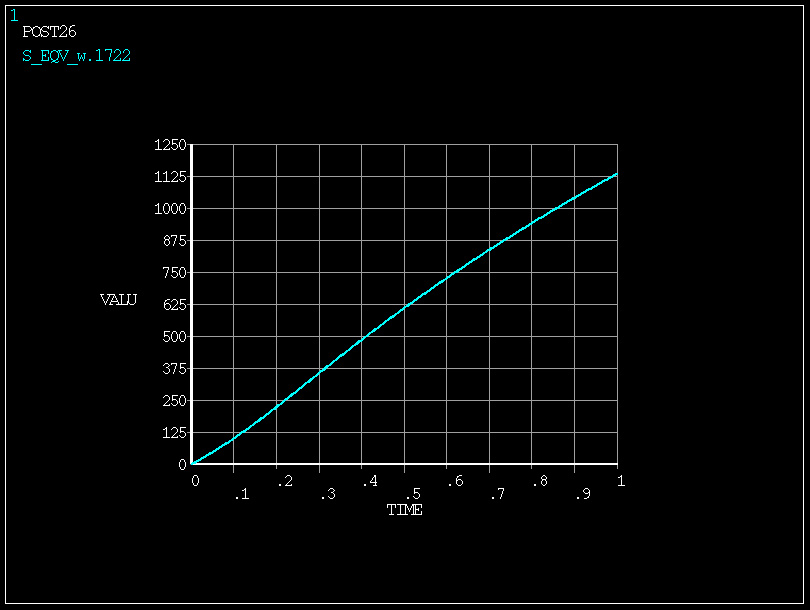
Konstrukcja zachowuje się nieliniowo, ale nie utraciła stateczności

.... ale po przyłożeniu dodatkowego obciążenia:

/SOLU
ACEL,0,9.81,0
FK,2,FY,-300
FINISH

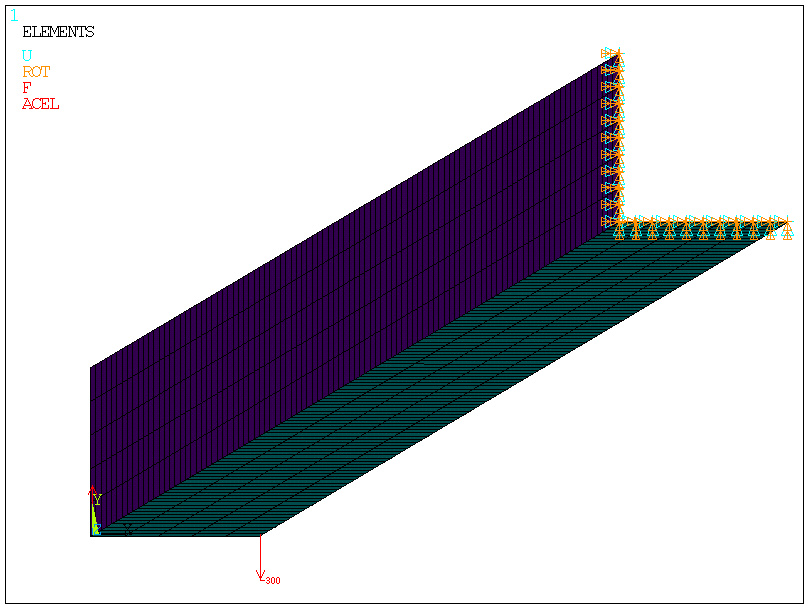
obliczenia zatrzymały się po 15 podkrokach

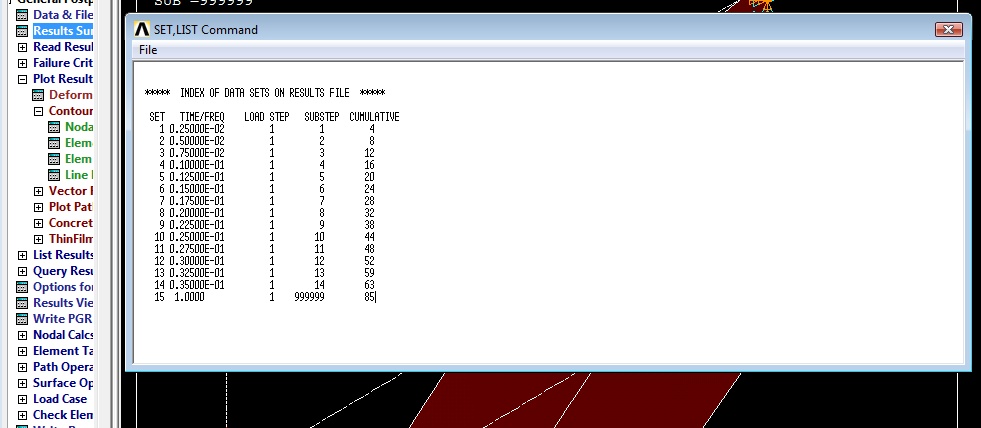
utrata możliwości dalszego pogłębiania obciążenia (zmiana obciążenia o kolejną 1/400 jest za duża, aby odgadnąć kolejne odkształcenie konstrukcji)

Algorytm automatycznego doboru kroku obliczeniowego

/SOLU
ANTYPE,0 ! analiza statyczna
NLGEOM,ON
AUTOTS,ON
NSUBST,5,5000,5 ! podział obliczeń na podkroki obliczeniowe (początek, max, min)
OUTRES,ALL,ALL
FINISH

ustalanie siły krytycznej

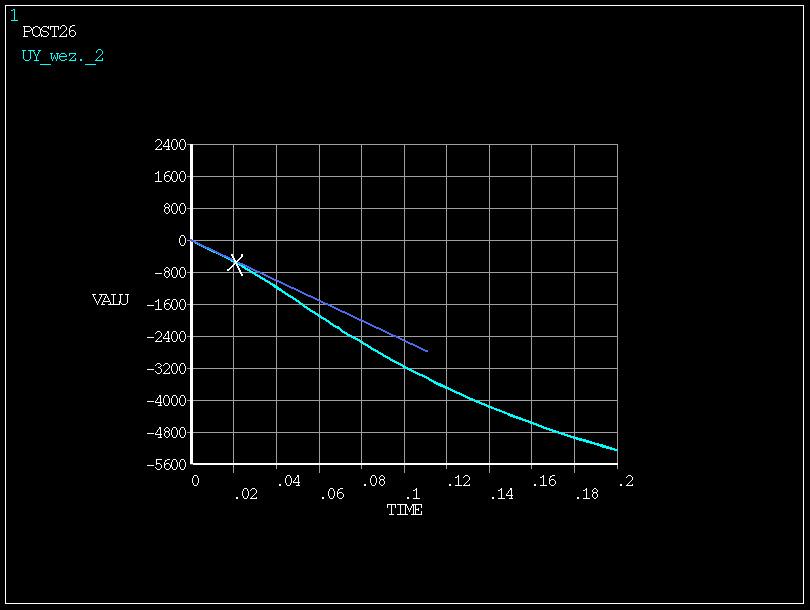
Fkryt=0.02.Fzad

stan po pełnym obciążeniu zadanym: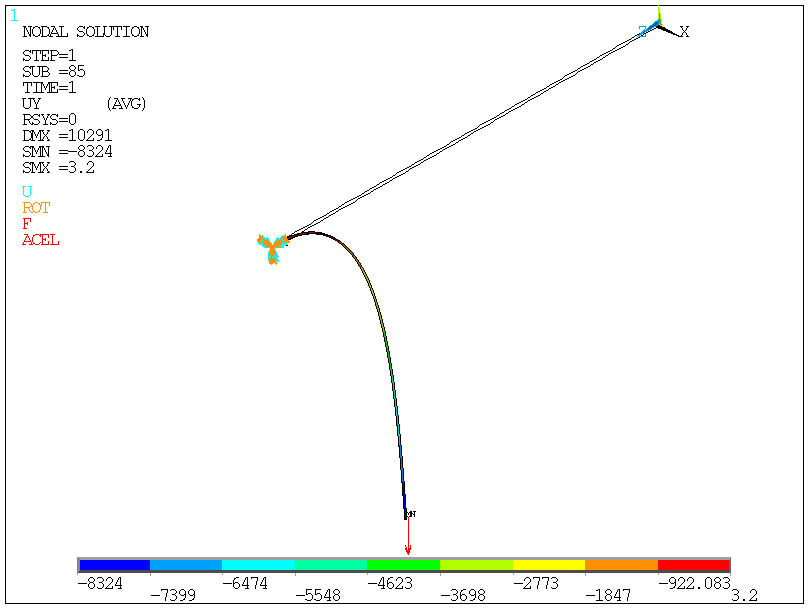

Stan w chwili utraty stateczności - obciążenie Fkryt=0.02.Fzad

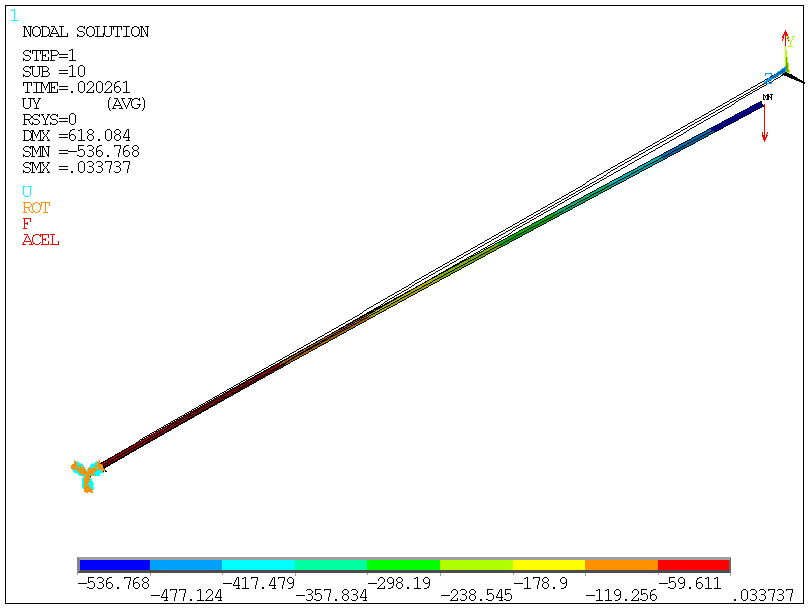
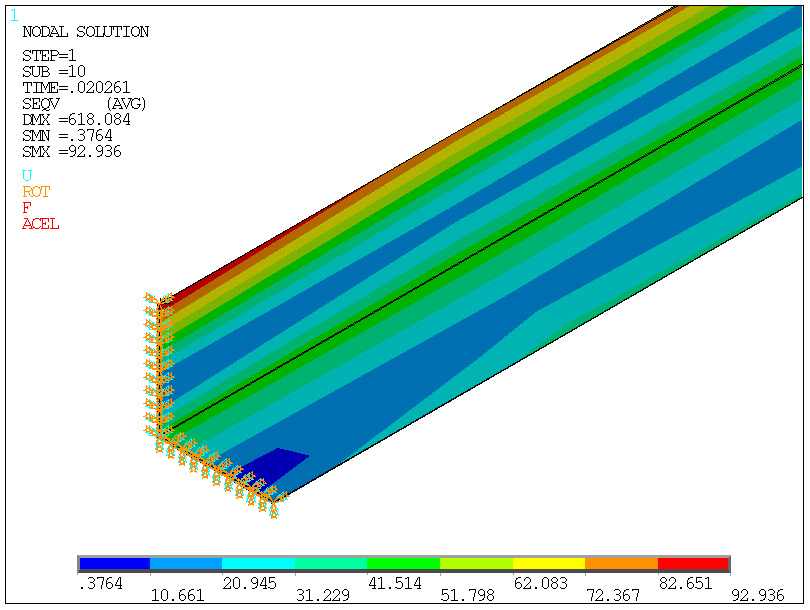
Utrata nośności nie z powodu dużych naprężeń, a z powody zwichrzenia!

Treść zadania obliczeniowego analogiczna do zad.1., przy czym:

ograniczono model geometryczny do powierzcniowego,
model MES bryłowy zastąpiono modelem powłokowym
zastosowano obciążenie i podparcie charakterystyczne dla stopni swobody elementu powłokowego
obliczenia skonfigurowano dla uwzględnienia dużych przemieszczeń (plik duze.mac)
nowa technika obrazowania wyników (plik film.mac)
badanie utraty stateczności (plik wykres.mac)